0:00
hi there welcome to we learn daily in
0:02
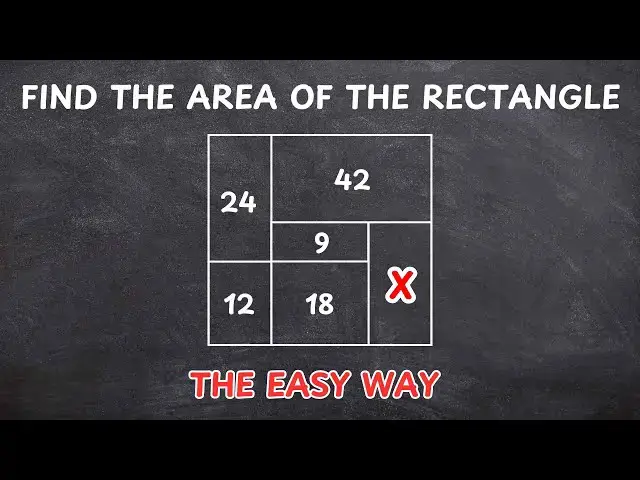
this video we will find the area of the
0:04
rectangle in the image if the areas of
0:06
the other rectangles are 24 42 9 12 and
0:12
18 square units as usual before watching
0:16
try to solve this problem on your own
0:18
now we'll go over an amazing method that
0:20
allows even a fifth grader to quickly
0:23
and easily solve any seemingly complex
0:25
problem of this type let's start by
0:27
considering the simplest case we'll take
0:30
a rectangle and divide it into four
0:32
smaller rectangles using lines parallel
0:34
to its adjacent sides we'll label the
0:37
areas of the smaller rectangles as S1 S2
0:42
S3 and S4 will prove that the areas
0:47
proportion S1 / S3 = S2 / S4 if we reite
0:54
this in terms of the fundamental
0:56
property of proportions we get that the
0:58
product of the outer terms
1:00
S1 * S4 must equal the product of the
1:04
inner terms S2 * S3 let's quickly prove
1:09
this we'll label the segments formed by
1:12
the division of the rectangle as a b c
1:16
and d then the area of the first
1:19
rectangle is equal to B * C the area of
1:22
the second rectangle is b multili d the
1:25
area of the third is a multiplied C and
1:29
the area area of the fourth is a * D
1:33
this means that S1 * S4 = B * C * a * D
1:40
and this product is the same as that of
1:42
S2 * S3 thus the property of the areas
1:46
is proven so when dividing any rectangle
1:49
into Parts with two lines the product of
1:52
the areas of the smaller rectangles
1:53
along one diagonal equals the product of
1:56
the areas along the other diagonal now
1:58
we'll use this property to solve our
2:00
problem first we'll extend the side of
2:02
the small rectangle with an area of nine
2:04
like this as a result we obtain a
2:06
rectangle for which we can apply the
2:08
area property we just proved if we
2:10
denote the unknown area of the new small
2:12
rectangle as s then according to the
2:14
area property the product of the areas
2:17
along one diagonal 18 * s must equal the
2:22
product of the areas along the other
2:24
diagonal 9 multiplied by 12 dividing
2:28
both sides by 18 we get S = 99 * 12 / 18
2:34
simplifying we get s = 6 therefore the
2:37
area of the new small rectangle is 6 if
2:40
we subtract this area from the rectangle
2:42
with an area of 24 we get 24 - 6 which
2:46
equals 18 this means the area of the
2:49
remaining part of the rectangle is 18
2:51
now we have another simple case of
2:53
dividing the largest rectangle into four
2:56
parts for which the area property holds
2:58
the product of the are areas along one
3:00
diagonal the yellow rectangles must
3:03
equal the product of the areas along the
3:05
other diagonal the blue rectangles
3:08
taking one yellow rectangle we add 9 and
3:11
18 to its area getting x + 9 + 18 and
3:15
multiply this by 18 this must equal the
3:18
product of the areas of the two blue
3:20
rectangles 6 + 12 multiplied by 42 we
3:24
combine like terms in the parentheses on
3:26
the left side and get x + 27 * 18 and
3:31
all of this should equal 6 + 12 which
3:36
42 we then divide both sides by 18
3:40
simplifying the equation we get x + 27 =
3:45
42 solving for x we find that x = 42 -
3:50
27 therefore x = 15 the area of the
3:55
rectangle in the image is 15 square
3:57
units the problem is solved if the
4:00
solution is clear give it a like leave a
4:03
comment and don't forget to subscribe to
4:05
the channel thank you for watching and
4:08
let's see you in the next video goodbye