Você sabe de onde vem a famosa fórmula de Bhaskara? 🤔
Muita gente só decora a expressão para resolver equações do 2º grau, mas não entende como ela é deduzida. Nesse vídeo eu mostro, passo a passo, a dedução da fórmula de Bhaskara de um jeito claro e direto. ✍️📐
Se você é estudante, professor ou apenas curioso por matemática, esse vídeo vai te ajudar a enxergar a lógica por trás da fórmula mais usada nas escolas.
Seja membro deste canal e ganhe benefícios:
https://www.youtube.com/channel/UCDeH_YvAsW0x1Qnkv8EZTuw/join
Show More Show Less View Video Transcript
0:01
Olá, seja muito bem-vindo ou bem-vinda.
0:05
Eh, eu me chamo Marcos e eu sou
0:07
professor de matemática recém formado e
0:10
eu tava aqui refletindo sobre quando a
0:14
gente estuda equação do segundo grau no
0:18
ensino fundamental,
0:20
o nono ano normalmente, né? E maioria
0:23
das vezes a gente só decora a fórmula,
0:27
porque no geral é o é o que a gente pode
0:31
fazer com o conhecimento matemático que
0:33
a gente tem naquele momento, né? Eu
0:36
acredito que
0:38
não é nem nem adequado fazer
0:40
demonstração
0:42
nessa nessa fase do ensino,
0:45
mas talvez se você decorou essa fórmula
0:49
e você se pergunta, né, de onde que vem
0:53
e como que surgiu isso, talvez esse
0:57
vídeo seja legal para você, né? Então, o
1:00
que que é uma equação de segundo grau?
1:02
Ela é uma equaçãoonde a gente tem esse
1:05
esse expoente do aqui, né, acompanhando
1:08
x. E ela geralmente é dessa fórmula, né?
1:12
Ax²
1:14
e + bx. Deixa eu pegar isso daqui. Ela é
1:18
dessa fórmula x² + bx + c = 0.
1:24
Eh, ela pode ser completa, né, que ela
1:26
vai ter todos os termos, né, ou pode ser
1:28
que ela não tenha aqui o BX, ou que ela
1:32
não tem aqui o C, né? E
1:35
mas ela precisa ter aqui o x qu ou ela
1:38
não vai ser o de segundo grau, né? Se se
1:41
esse a que for zero, por exemplo, né?
1:43
Isso aqui não vai ter. Isso aqui vai ser
1:45
simplesmente uma reta, né? Aqui tá bx +
1:48
c, mas ela seria a mesma coisa que um ax
1:50
+ b, né? Que é uma reta.
1:52
Então aqui a gente vai, gente, vou olhar
1:55
aqui algumas coisas primeiro
1:57
que a gente vai precisar eh para fazer
2:00
essa essa solução, essa demonstração e
2:03
encontrar a fórmula dela, né? Primeira
2:06
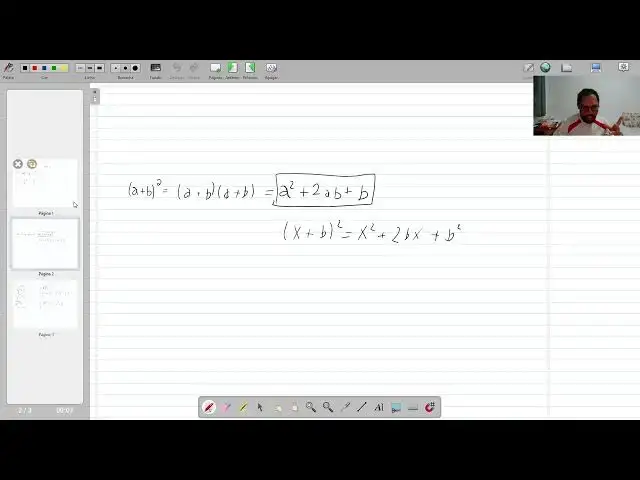
coisa é saber esse produto notável aqui
2:09
que é a + b².
2:11
É isso aqui talvez em algumas pessoas
2:13
possa gerar uma confusão e
2:17
talvez a pessoa achar que isso daqui é a
2:19
quad + b², porque isso aqui é a + b²,
2:24
né? E
2:27
na verdade isso daqui você tem que
2:28
aplicar distributiva, né? Então você vai
2:30
fazer isso daqui a + b
2:35
vezes
2:37
a + b.
2:39
E quando você fizer a x a, isso aqui vai
2:41
ficar a quadrado.
2:43
E aí você vai fazer a x b.
2:48
B x a ab também. Então vai ficar 2ab.
2:54
E b x b vai ficar b².
2:58
Então esse aqui é o produto notável que
3:00
a gente precisa.
3:03
Esse aqui é um produto notável bem bem
3:05
comum, né, que aparece bastante, então é
3:07
importante saber. E eu tô revisando ele
3:10
aqui especificamente, porque a gente vai
3:12
usar ele para para resolver e demonstrar
3:16
ali a equação de segundo grau, a solução
3:18
dela.
3:20
E tem uma outra coisa também que gera
3:22
muita confusão, e isso daqui talvez seja
3:25
o mais importante,
3:27
que é
3:30
essa diferença entre a função y² = x e a
3:35
raiz quadrada.
3:36
É porque o que que acontece?
3:39
muita, existe muita confusão sobre sobre
3:43
a raiz quadrada de um número eh ser ou
3:46
não ser um número positivo ou um número
3:48
negativo, né? Porque quando eu falo
3:50
aqui, por exemplo, quadrada de 4, só que
3:54
é igual a 2.
3:56
Eh, por quê? Porque 2 qu 2²
4:00
é igual a 4. Só que -2
4:05
-2²
4:07
também é igual a 4. E aí você pode se
4:10
perguntar por que que -2 não é √4
4:14
também, né?
4:16
E e aí se você pegar em um livro
4:19
didático, eh, eu acredito que a maioria
4:21
dos livros tragam essa definição, mas a
4:24
raiz quadrada ela é definida
4:26
como raiz quadrada de a = b, sendo que a
4:31
e b são maiores que zero, né? Ou seja,
4:33
são números positivos.
4:35
E tal que b² ig a. Então o b tem que o
4:40
b² tem que ser o número que ele é igual
4:41
ao A, né? para eles ser a raiz e eles
4:43
têm que ser maior do que zero. Ou seja,
4:45
a gente sempre vai pegar o número
4:46
positivo. Só que quando a gente olha
4:48
para essa função y², que é igual a x, aí
4:52
realmente, né, se
4:55
se aqui eu tiver alguma equação
4:58
que
5:02
que x²
5:04
é igual a 4, o que acontece é que quando
5:07
a gente vai resolver, a gente
5:09
normalmente faz isso daqui, né? a gente
5:11
coloca aqui x = √4
5:15
e aí a gente coloca que isso daqui
5:18
é igual a
5:21
a 2. Só que nesse caso aqui, como isso
5:24
aqui é uma função,
5:26
quando eu aplico
5:29
para eu resolver isso daqui, na verdade,
5:32
o que eu tô fazendo é que eu estou
5:34
aplicando
5:36
a raiz de ambos os lados da equação. E
5:39
quando eu faço isso,
5:42
eu vou ficar aqui x é igual a mais ou
5:45
menos √4.
5:47
E aí aqui sim que eu vou usar os dois
5:49
valores, porque pr essa função tanto -2
5:54
quanto 2 são solução, né? Porque os dois
5:56
elevados ao quadrado vão dá 4. Então
5:59
existe essa confusão entre a raiz e a
6:02
função. E isso aqui vai ser importante
6:05
porque em algum momento ali da solução
6:08
vai aparecer essa estrutura e é por isso
6:11
que que que lá na solução aparece um
6:15
mais ou menos raiz de delta, né? aquilo
6:17
lá não é porque a raiz ela é positiva e
6:20
negativa. A raiz do delta é um número
6:22
positivo. Só que aquele mais ou menos
6:24
ele vai aparecer porque por causa dessa
6:27
função y qu. Então
6:30
vamos começar, né? Agora que a gente já
6:32
esclareceu essas coisas, vamos vamos lá.
6:37
Eh, bom, como a gente já falou no
6:39
começo, a gente tá assumindo que que o A
6:43
é diferente de zero. Então, a primeira
6:45
coisa que eu vou fazer aqui é dividir
6:49
tudo por a.
6:51
Eh, então aqui x²
6:54
+
6:56
b,
6:59
ops,
7:02
b/ a
7:05
x.
7:07
+ c sobre a ig 0. Eh, se esse a fosse
7:13
zero, né, que eu teria uma divisão de
7:14
zero sobre zero, eu já teria uma
7:16
indeterminação, né, então já daria um
7:18
problema. Mas ao mesmo tempo não faz
7:21
sentido eu pensar nisso daqui como um a
7:24
igual a 0, porque se o a fosse zero,
7:26
esse termo aqui a x², ele nem existiria
7:29
e aí nem faria sentido fazer essa essa
7:32
resolução, né? Porque isso aqui nem
7:34
seria uma equação do segundo grau.
7:37
Então aqui é vamos observar uma coisa,
7:40
né? Eu vou eu vou passar esse esse C
7:44
sobre A pro segundo membro para ficar um
7:46
pouco mais claro aqui o que o que que eu
7:49
quero que vocês observem.
7:52
Então aqui, ó, eu tenho esse B sobre A
7:56
vezes X. Isso aqui vai ser igual a - c
8:01
sobre A. É isso daqui é um x²
8:06
+ um termo que tá multiplicando x.
8:10
Se a gente olhar aqui pro produto
8:11
notável,
8:13
a gente tem que isso daqui é um ao
8:14
quadrado
8:16
mais um termo que multiplica
8:20
eh 1 a x b + b. Vamos imaginar que isso
8:24
daqui fosse
8:27
alguma coisa do tipo x
8:31
+ b²,
8:33
né? Ao invés de a + b. Então isso daqui
8:36
seria x²
8:38
+ 2
8:41
b x
8:45
+ b².
8:47
Então pera aí. Então esse daqui
8:50
seria 2 bx. Então assim já deu uma coisa
8:55
assim mais ou menos parecida, né? Então
8:58
eu tenho que encontrar,
9:00
vou tentar encontrar aqui algum termo
9:03
que eu possa, que duas vezes ele seja b
9:08
a x.
9:10
E depois da gente tentar aqui um
9:12
pouquinho,
9:14
a gente percebe que
9:17
que esse termo ele pode ser b/ 2a, né?
9:21
Porque quando eu multiplicar
9:23
isso daqui por 2
9:26
e por x, isso daqui vai ficar
9:31
2 x b.
9:35
Opa, esse dois aqui vai embora, né? Isso
9:37
aqui vai ficar b a x.
9:42
Então, pera aí.
9:44
Então, quer dizer que eu consigo fazer
9:48
esse termo aqui aparecer
9:52
como um quadrado. Então, vou fazer ele
9:54
aqui do lado, né? Então, vamos fazer
9:56
aqui, ó, como que seria? X
10:01
+ b
10:04
sobre 2a
10:06
a quadrado. Vamos ver o que que
10:08
acontece. Eu vou vou passar um um traço
10:11
aqui pra gente não misturar as coisas.
10:14
Então vai ficar isso aqui ficar isso
10:15
aqui seria x²
10:18
+
10:20
2 x x b x 2a.
10:24
O 2 vai cortar com o 2. Então vai ficar
10:28
b
10:30
sobre a x +
10:33
é b².
10:39
sobre 2² 4
10:42
a quadrado. Opa, pera aí. Parece que em
10:45
algum lugar da fórmula de báscara
10:47
aparece b², aparece 4a. Já tá começando
10:52
a me ficar familiar isso daqui, né?
10:55
Então, bom, acho que a gente tá no no
10:57
caminho certo disso daqui.
11:00
Só que perceba que isso daqui, ó, isso
11:04
daqui aparece aqui,
11:06
só que ainda tá faltando, vou até pegar
11:09
um vermelho aqui,
11:12
falta aparecer esse termo aqui.
11:16
E se a gente lembrar das propriedades da
11:19
das equações, se eu somo um termo dos
11:22
dois lados da equação, eu não altero a
11:24
minha igualdade. Então o que que eu vou
11:26
fazer? Eu vou somar
11:30
esse termo aqui dos dois lados da
11:32
equação
11:34
para que apareça esse
11:38
essa coisa inteira aqui
11:41
desse lado aqui. Então o que que eu vou
11:43
fazer?
11:44
x²
11:46
+
11:48
b/ a.
11:52
Opa,
11:55
b a x
11:58
+
12:01
b²
12:03
sobre
12:07
4a²
12:10
igual. Aí vou somar aqui de novo do
12:13
outro lado, né?
12:14
b²
12:16
sobre
12:18
4A²
12:20
menos esse C sobre A.
12:23
Então, perfeito, né? Eu somei dos dois
12:25
lados da equação, então não alterei a
12:27
igualdade.
12:29
Agora perceba que apareceu todo esse
12:33
produto notável aqui, ó. X² X² X²
12:37
BX/ A BX/ A B²
12:42
sobre 4². Então eu posso trocar esse
12:46
termo aqui inteiro por x + b/ 2a elevado
12:51
ao quadrado. Então deixa eu descer essa
12:55
folha aqui um pouquinho. Ops.
12:58
Cadê aqui a mãozinha?
13:02
descer só até aqui pra gente não perder
13:04
ali que a gente tava fazendo. Então
13:07
agora eu vou trocar isso daqui por x +
13:15
b
13:17
sobre 2a.
13:19
Isso aqui é tudo ao quadrado
13:23
igual
13:26
AB²
13:28
sobre
13:30
4a²
13:34
- c
13:36
sobre a. E lembra que eu falei que em
13:39
algum momento ia aparecer
13:42
e um y² = x? Se a gente observar aqui
13:46
essa estrutura aqui, ó, ela é muito
13:48
parecida com y²
13:51
= 1 x. Então, repara a semelhança, né,
13:55
daquilo lá com isso daqui.
13:59
Então,
14:01
eh, daqui a pouco a gente vai usar isso,
14:03
que eu ainda não vou isolar esse
14:08
esse termo, fazer mais um passo antes,
14:10
mas já repara a semelhança, né? Aqui a
14:13
gente já tá bem avançado na na solução.
14:17
Agora o que que o que eu vou fazer é só
14:19
juntar esses termos do segundo membro
14:22
para ficar um pouco mais organizado, né?
14:24
Então aqui, vamos lá. X
14:29
+ B
14:32
sobre 2a
14:34
elevado ao quadrado é igual. E, eu quero
14:37
somar essas duas frações, então eu vou
14:40
fazer aqui um mínimo múltiplo comum, né?
14:43
Então eu vou eu vou simplesmente
14:47
mínimo múltiplo comum de 4a² e de a vai
14:51
ser 4a ao quadrado, né? Porque o a é
14:56
múltiplo de 4a².
14:59
E aí eu vou dividir 4a² por a vai ser
15:04
4a,
15:07
então vai ficar
15:10
e
15:13
4
15:16
AB
15:18
ao quadrado.
15:23
E
15:25
ops, opa, aqui eu já fiz errado. Calma
15:28
lá.
15:32
Peço desculpas pela minha desatenção.
15:38
Eh, 4a
15:40
4a² dividido por 4a² vai dar 1, né?
15:43
Então isso aqui vai ser b²
15:46
- 4a² dividido por por a vai ficar só
15:50
4a. Então isso aqui vai ser b² - 4ac.
15:56
É, B² - 4ac, a gente já conhece de de
16:01
algum lugar, né? Se você conhece a
16:02
fórmula, você já sabe até o nome desse
16:05
desse termo, né? Como que ele qual que é
16:07
o apelido que ele tem, né? Então agora
16:10
que que a gente vai fazer?
16:12
Agora a gente vai é tirar a raiz
16:14
quadrada dos dois lados da equação.
16:16
Então o que a gente vai fazer?
16:18
A gente vai fazer que x +
16:22
b sobre 2a
16:27
vai ser igual
16:29
a mais ou menos. Então, veja bem, é
16:32
nesse momento que
16:35
que aparece aqui esse mais ou menos, né?
16:39
A raiz.
16:43
Peço perdão pela minha habilidade de de
16:45
escrita de no computador, porque ela é
16:48
muito ruim ainda, né? B quadrado
16:51
-
16:53
4ac
16:56
dividido por
16:59
4a².
17:00
E aqui a gente lembra de uma
17:02
propriedade,
17:04
eh,
17:05
vou até fazer ela aqui na na outra
17:08
folha, que existe uma propriedade das
17:12
das raízes que ela é assim, né, que é a
17:14
raiz de A sobre a raiz de bode escrever
17:18
como ra
17:21
dividido por √ b. É exatamente isso que
17:24
a gente vai usar aqui para poder separar
17:28
esses dois termos, né? Então aqui agora
17:30
já não precisa mais desse parênteses,
17:32
né? a gente vai ficar x + b sobre 2a vai
17:39
ser igual a mais ou menos
17:43
raiz
17:45
de b²ad
17:52
4
17:56
ac
17:59
é dividido pela raiz
18:05
de 4 a quadrado
18:09
e a raiz de de 4² a gente sabe calcular,
18:12
né?
18:14
Então,
18:16
x + b/ 2a é igual a mais ou menos
18:23
raiz
18:25
de b
18:28
quadrado
18:31
- 4ac
18:35
é √4 vai ser 2 √ a² √² vai ser a.
18:42
E aí agora para finalizar a gente chega
18:44
aqui que x vai ser igual
18:48
eh esse b sobre 2a ele vem para cá
18:51
negativo, né? Então, - b
18:56
sobre 2a
19:00
mais ou menos
19:04
raiz
19:06
de b²
19:11
- 4ac
19:15
sobre
19:17
2a.
19:18
É, o que acontece é que aí a gente
19:20
carinhosamente apelida esse
19:25
é esse B quadrado ali
19:29
b qu
19:33
de delta. Aí fica um pouco mais simples
19:36
de escrever, mas esse termo aqui é o que
19:38
a gente aprende normalmente como delta,
19:41
né? A gente aprende a calcular o delta
19:43
separado, né? Que é a variação dessa
19:46
dessa raiz.
19:48
E a gente normalmente também junta isso
19:51
daqui, né? Mas no a solução é isso
19:54
daqui.
19:56
Então
19:58
é, se você resolver dessa maneira, você
20:01
chega nessa resolução aqui.
20:04
E aí você quiser ser um pouquinho mais,
20:09
é preciso você ser junto aqui, né?
20:12
mais ou menos b²
20:16
- 4ac, né? Também poderia ter escrito o
20:20
delta aqui, né?
20:23
Ops.
20:25
[Música]
20:29
Deixa eu tirar isso daqui.
20:36
Poderia ter colocado aqui.
20:41
Deixa eu apagar isso daqui.
20:43
Podia ter colocado mais ou menos raiz de
20:45
delta. Delta tá tá aqui, né?
20:50
E aí, como é o mesmo denominador,
20:55
você junta aqui o 2a, né? E aí vai ficar
21:00
eh - b mais ou menos√ delta sobre 2a. E
21:05
essa é a solução da da equação do
21:08
segundo grau.
21:10
Lembrando que você pode resolver a
21:11
equação do segundo grau desse jeito
21:13
também, tá? Tem tem professor que você
21:16
vai ver resolver desse jeito. Tem muita
21:17
gente que que não gosta às vezes de usar
21:19
a fórmula, né? E aí resolve dessa
21:21
maneira, mas você tinha aí curiosidade,
21:24
tinha decorado a fórmula, é desse jeito
21:27
que você chega aí na na equação de
21:30
segundo grau, na fórmula para resolução.
21:34
E lembrar aí dessas propriedades, né?
21:37
Sabendo aí
21:39
pros notável essa propriedade aqui das
21:44
das raízes, né, que a raiz de A sobre b
21:47
=√ a sobre a rab. Sabendo, entendendo
21:51
também
21:52
eh
21:54
que quando você tira a raiz dos dois
21:56
lados da equação, aparece esse mais ou
21:58
menos, você entende de onde vem esse
22:00
mais ou menos e que ele não é
22:03
eh pertencente ao delta, né? é esse
22:07
valor aqui, né? Ele é pertencente
22:10
a esse momento que você faz essa
22:12
passagem dessa função aqui, né, que
22:14
seria equivalente a 1 y qu, né, porque
22:17
ao passar desse lado para esse, né, e
22:19
tirar essa raiz dos dois lados, você tem
22:21
que considerar tanto a parte positiva
22:23
quanto a negativa, né, para você ter as
22:25
duas raízes. É porque isso daqui toca o
22:29
eixo em dois pontos, né? Essa função y
22:31
qu ela também, né, ela vai ter dois
22:34
valores que vão ser solução.
22:37
É, então é isso. Espero que você tenha
22:39
gostado
22:41
e e bons estudos para você. Até a
22:43
próxima.