0:02
now the slope of the tangent at any
0:04
point on the curve but we want the slope
0:06
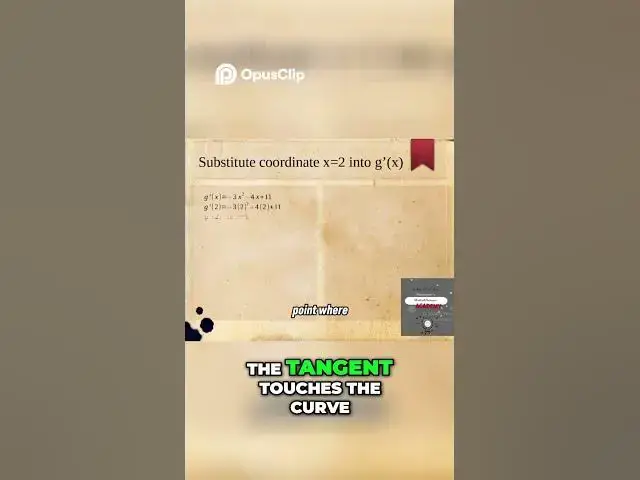
at x= 2 so g prime of 2 = -3 * 2 ^ 2 - 4
0:11
* + 11 = 2 - 12 - 8 + 11 =8 so the slope
0:17
of the tangent at point x = 22 is8
0:21
now the next thing we need to do is to
0:22
substitute the xcoordinate x= 2 into the
0:25
original function gx and that will give
0:27
us the y-coordinate of the point where
0:29
the tangent touches the curve so let's
0:31
go ahead and do that now so we have g2
0:33
is equal to 2 cub 62 ^2 + 92 so that's
0:37
equal to 8 - 24 + 18 which is 2 so
0:41
that's the y-coordinate so the point has
0:43
the coordinates 2 2 okay so that's the
0:45
first step find the gradient and the
0:47
second step is to substitute the
0:49
xcoordinate into the original function
0:51
to find the y-coordinate