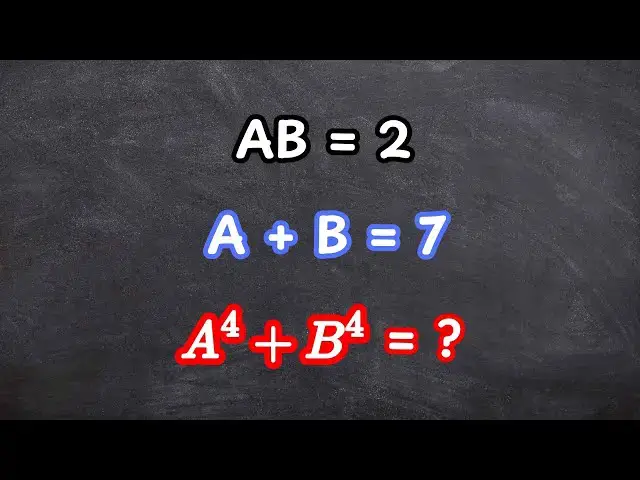0:00
the product of A and B is equal to 2 and
0:03
the sum of A and B is equal to
0:06
7 find the sum of the fourth powers of A
0:11
B as usual pause the video and try to
0:14
solve the problem yourself we begin with
0:16
the standard formula for the square of a
0:18
sum A + B which is equal to the square
0:21
of the first term plus the square of the
0:23
second term plus twice the product of A
0:26
and B we subtract twice the product of A
0:29
and B from the square of the sum and we
0:31
express the sum of the squares a 2 + b 2
0:34
we get the sum of a 2 and b^2 = a + b^ 2
0:40
- 2 * a b now let's write the same
0:44
formula but for the square of the sum of
0:46
the squares of A and B that is instead
0:49
of a we take a squ and instead of B we
0:52
take B squared by the same formula it
0:55
will be equal to the square of the first
0:57
term plus the square of the second term
0:59
Plus twice the product of the squares
1:01
when raising a power to a power the
1:03
exponents multiply so a squar or squared
1:06
becomes a to the 4th and b^ 2 all SAR
1:10
becomes B to the 4th we subtract twice
1:13
the product of the squares of A and B
1:15
from the square of the sum of the
1:16
squares and we express the sum of the
1:18
fourth powers of A and B we get the sum
1:21
of a to the 4th and B to the 4th equal
1:24
the square of a 2 + b^ 2 - 2 * a 2 b^ 2
1:29
we replace the sum of the squares of A
1:31
and B with the difference we get a + b -
1:34
2 and all of this squared minus 2 * the
1:38
product of the squares of A and B
1:40
alternatively this can be written as 2 a
1:43
b and all of this squared by condition
1:47
the sum of a and b equals 7 and the
1:50
product of a and b equals 2 substituting
1:54
these values we get 7^ 2 - 2 * 2 and all
1:58
of this SAR - 2^2 which = 45 - 8 to find
2:03
the square of such a number for example
2:05
for 252 we multiply two by the next
2:08
number three and add 25 which gives us
2:12
625 similarly for 75 squ we multiply 7
2:17
by the next number 8 giving 56 and we
2:19
add 25 in the same way we can find the
2:22
square of a three-digit number for
2:24
example 9995 we take 99 multiply it by
2:28
the next number 100 get 99,900 and add
2:34
9,925 so to find 45 squared we multiply
2:38
four by the next number five getting 20
2:41
and we add 25 giving 2025 - 8 which
2:45
equal 27 the answer is the sum of the
2:49
fourth powers of a and b equals
2:52
2017 the problem is solved if you
2:56
understood the solution like the video
2:58
leave a comment and don't forget to
3:00
subscribe to the channel