Understanding The Extreme Value Theorem, Critical Numbers, Absolute Minimum & Maximum
Feb 19, 2025
If you need tutoring help, visit https://dothatmath.com/
We will be discussing the Extreme Value Theorem, Critical Numbers, Absolute Minimum & Maximum. This theorem is important in Calculus and Analysis. It basically states that given a function defined on a closed interval, there must exist a maximum and minimum value of the function on that interval. We will be discussing what these terms mean and how to find them.
Show More Show Less View Video Transcript
0:00
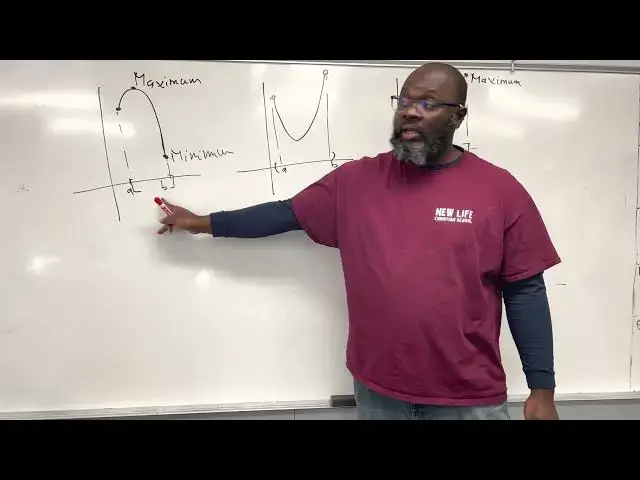
look at the ball here
0:02
so I have three
0:04
separate functions right and I want you
0:06
to recognize some patterns here so if
0:08
you go from right to left so what do you
0:12
see here
0:13
about this function
0:16
absolute value right it looks like a V
0:20
what would you call this point
0:23
it's the highest point right
0:25
maximum maximum it's a maximum right
0:27
it's a maximum
0:30
right we have a maximum here
0:32
and what you call this here
0:36
there's nothing that's a whole right so
0:38
the function is undefined so there's
0:40
nothing there right we don't have
0:43
anything there and this is just another
0:44
point on the graph correct and what
0:48
would you say about this function
0:50
it is only one a closed animal right
0:54
between A and B do you see that now
0:57
second what do you see here
1:00
any observations
1:05
that's not defined point right it's the
1:07
open envelope so it's open right it
1:09
doesn't end here so we're gonna have
1:11
parenthesis here we're going to have a
1:13
bracket
1:14
right
1:16
and what else do you see here there's a
1:18
function of a maximum
1:20
does it it doesn't
1:22
it's a circle that inside so open circle
1:25
it doesn't end here right it's not a
1:27
close animal what's the point under that
1:30
if he was close though there would be a
1:32
maximum it's an open circle
1:34
so there's no maximum there there's a
1:36
hole right
1:39
you see that now the last one what do
1:41
you notice
1:42
what do you have here
1:45
yeah the function is on the closed
1:48
interval right
1:50
it's a bracket
1:51
then what do you have here what would
1:53
you call this here
1:55
minimum right
1:57
minimum
1:59
and then this will be a
2:01
you use the term maximum or in this case
2:04
since it looks like a parabola a Vertex
2:06
right but it's a maximum right
2:08
so now what can you establish
2:11
about a maximum and a minimum on a
2:14
closed angle what would you say
2:17
maximum is the highest points let's play
2:20
well that's obvious right but for that
2:23
to happen
2:24
there has to be two conditions that have
2:26
to be met right the function has to be
2:29
what first continuous
2:31
right continuous because here's it's
2:34
continuous and then what else
2:36
it has to be bounded right it has to be
2:41
a closed animal does that make sense so
2:44
if
2:46
so this is called the mean
2:49
mean value
2:55
right mean value term in a sense that if
3:01
is a continuous function
3:09
on
3:10
the closed
3:12
interval
3:16
a b
3:18
then we conclude that the conclusion is
3:22
foreign
3:42
right does that make sense so if f is a
3:45
function and F is a continuous function
3:47
on a closed interval so this is always
3:50
going to be true f is going to have both
3:52
a maximum n minimum value now in this
3:56
case the close the interval is closed
3:59
but what the function is not what it's
4:01
not continuous right there's a gap here
4:03
there's a hole here so it's not
4:05
continuous so therefore F only has a
4:07
maximum it does not have a minimum in
4:10
case number two the function
4:12
heart is not on a close animal it's on
4:15
an open animal right A and B are not
4:17
included it's continuous but it's not on
4:19
a close animal and then the third one
4:22
you have a and b it is closed and then
4:25
the function is continuous completion
4:27
and it's both
4:28
a maximum and minimum value does that
4:31
make sense
4:32
any question on that
4:34
all right so now we're going to jump
4:35
onto from that to like relative maximum
4:39
and relative extremas now
4:41
if you have a function give you a
4:43
different function here
4:51
did you guys do um maximums and critical
4:54
numbers in pre-calculus
4:57
or not not at all yes no all right
5:01
so let me give you this function here
5:05
right
5:08
so what you have here is not a problem
5:11
right it's a function
5:12
but then what do you notice about this
5:14
function
5:15
the other possible one a possible
5:18
maximum here right
5:21
so maximum possible
5:25
Max
5:26
and this is what
5:28
a possible
5:32
minimum
5:33
right and then another possible Max
5:39
so what can we draw from this we can say
5:42
that this is an open interval because
5:43
there's no there's no end right it does
5:45
not end anywhere it keeps going from
5:48
negative Infinity right to positive
5:51
Infinity does that make sense
5:54
this is not a closed antibody function
5:56
it keeps going all the way to Infinity
5:58
all the way to Infinity here so what are
6:01
some conclusions that we can make here
6:03
we can call this a relative maximum and
6:07
this is also what we call a relative
6:09
minimum meaning on this on on the entire
6:12
open interval you have the possible
6:15
minimum here you have a possible maximum
6:17
and you have another possible maximum so
6:19
those are called relative
6:21
it depends on how you define that
6:23
function right so if I were to cut this
6:25
function from here to here this will be
6:27
a maximum if I have to cut this function
6:29
from here to here this will be a maximum
6:31
and this will be a minimum so those are
6:33
called relative extremas okay relative
6:38
relative
6:40
extrema
6:42
you know people usually say truth is
6:44
relative truth is relative meaning your
6:46
truth is not my truth so a relative
6:49
maximum is basically one possible
6:52
maximum does that make sense and a
6:54
relative minimum is one possible minimum
6:56
okay
6:58
so you have a relative maximum
7:05
and any relative
7:09
minimum
7:12
this is on on open
7:16
interval okay that happens now
7:20
this is the case with parabolas this is
7:22
the case with like uh sometimes those
7:25
absolute value function you may have a
7:26
relative Max relative mean now we're
7:28
going to go from there to set up uh what
7:31
we call uh critical numbers and then
7:33
derivatives again we're back to the
7:35
rivers again
7:36
so did you write this down good all
7:40
right that are you good
7:44
so now we're going to talk about
7:47
critical numbers and relative
7:49
experiments so critical numbers
7:59
so how do you find a critical number and
8:02
what is a critical number so let's say
8:04
we have a function let's find a function
8:06
here that'll help us real quick
8:10
so if I have a function f of x
8:14
equals to 3x 34 minus
8:18
uh
8:20
4X cubed
8:22
over the integral
8:27
negative one
8:30
to two and the question is
8:33
um find the absolute Max and the
8:37
absolute mean of this function now a
8:40
natural Max is the highest number on on
8:44
the function for a function and an
8:45
absolute mean is the lowest value on the
8:49
function on a given closed animal right
8:51
so to find the absolute Max and the
8:54
absolute mean we have to use what we
8:55
call the critical numbers right so how
8:57
do you find the critical numbers you
8:59
first find the derivative of the
9:00
function find the derivative so what is
9:02
the derivative of this function
9:04
all right
9:06
what's the river
9:08
yes is it 12 x to the Third
9:14
minus 12x to the
9:17
second power second power so that's the
9:19
that's his first derivative now to find
9:23
the critical numbers you're going to set
9:26
the first derivative to zero and solve
9:29
for x and those values are called
9:31
critical numbers so we set this equal to
9:34
zero set the derivative
9:37
equals to zero so we have 12 x cubed
9:41
minus 12 x squared is equal to zero and
9:44
then we're going to solve for x right
9:46
I'm gonna put 12x Square as a factor
9:50
I'm going to be left with x minus 1
9:54
is equal to zero right so my critical
9:58
numbers are going to be I'm going to
10:00
have x squared equal to 0 and then x
10:02
squared minus 1 is equal to zero
10:05
so I have X is equal to zero and then X
10:08
is equal to one so those are called the
10:11
critical numbers
10:13
to find the critical numbers you set the
10:16
derivative equal to zero and you solve
10:18
for x yes
10:19
well 12 times 12 are just divided by 12
10:22
so it's gone right if I have 12x squared
10:25
you don't it doesn't really matter
10:26
because I'm going to divide by 12.
10:29
12 right so X is equal to zero
10:33
so the critical numbers miracle
10:37
numbers
10:40
are
10:42
0 and 1. now how do we use the critical
10:46
numbers so here's what we're going to do
10:48
right on this function here they want us
10:51
to find the absolute maximum and the
10:54
absolute minimum of this function now
10:57
that we found the critical numbers we're
10:58
going to use the critical numbers and
11:00
we're also going to use the end point of
11:02
the closed interval to see which one of
11:05
these values yield to the highest number
11:07
and yield to the lowest numbers and
11:09
those are going to be called absolute
11:11
mean and absolute Max respectively so
11:14
the next step now that we have the
11:16
critical numbers so we're going to take
11:18
each value here so we have
11:21
negative 1 right is the end point and
11:24
I'm zero
11:26
and then one and two so we're going to
11:28
evaluate the function at those given
11:30
points
11:31
and the one that gives us the highest
11:33
value is going to be called the absolute
11:35
Max and the one that gives us the lowest
11:37
is going to be called
11:38
the absolute mean so find f of negative
11:42
one you can you guys can use your
11:43
calculator find F of zero
11:46
find F of one and then find F of 2.
11:51
so obviously F of 0 that's going to give
11:54
us zero right just plug in 0 here so
11:56
that's going to be zero so what's f of
11:59
negative one f of negative one will be
12:01
three
12:02
negative one to the fourth minus four
12:04
negative one to the three
12:07
three and this start with three right
12:09
negative four and negative one that'll
12:12
be positive four
12:13
value positive seven
12:15
and then F of one will give you three
12:19
one to the fourth minus four one to the
12:22
third that is three minus four that's
12:26
negative one and then F of two I need
12:29
you you guys to help me with f of two
12:31
every three two three four
12:34
minus four two to the third what's that
12:37
gonna give you
12:44
what do you get for f of two
12:47
you do it
12:53
this is
12:54
three is sixteen right and then minus
12:57
four times two and two and two that's
12:59
eight
13:00
so that would be 3 and 16 is what
13:04
48 right minus 32 so that is uh 16. all
13:10
right so look here now we have 7
13:13
negative one eight on and then sixteen
13:16
and zero so which one do you think is
13:18
the absolute Max what value gives you
13:19
the absolute match here
13:23
yes
13:25
two right so this is absolute Max
13:29
is a two
13:32
and what's the absolute mean
13:34
foreign
13:36
gives us the absolute minimum
13:41
anyone
13:45
F of one right absolute minimum
13:54
so basically
13:56
to find an absolute minimum and the
13:58
absolute minimum minimum the actual
14:01
maximum of function on the on the closed
14:04
interval
14:05
you value the functions at the end point
14:08
right these are the end point and then
14:10
you find the critical numbers and
14:12
evaluate the function at all those
14:15
values and the one that gives you the
14:16
lowest value is the absolute name and
14:18
the one that gives you the highest value
14:20
is the absolute Max any question on that
14:23
any questions
14:25
no good so now we're going to work on
14:27
some problems in the book