
Gaussian Elimination to Solve a 3 by 3 System of Equations
This video has three objectives: 2 - Explains what is an augmented matrix 2 - Explains what is a matrix in row echelon form 2 - Use the Gaussian Elimination method to rewrite the augmented matrix in row echelon form 3 - Use back substitution to solve the

Inverse of a 3 by 3 Matrix Using Gauss-Jordan Method
This video goes through the steps in finding the inverse of a 3 by 3 matrix. There are three objectives 1 - Explain what is a matrix in reduced row echelon form (rref) 2- Write the augmented matrix of the equation to solve 3 - Use the basic row elementa

Solve 2 by 2 System of Equations by Elimination
This video shows how to solve systems of equations using the method of elimination. The two basic operations that may be used to rewrite the system of equations into an equivalent one (i.e.with the same solutions) are 1 - multiply equations by a constant
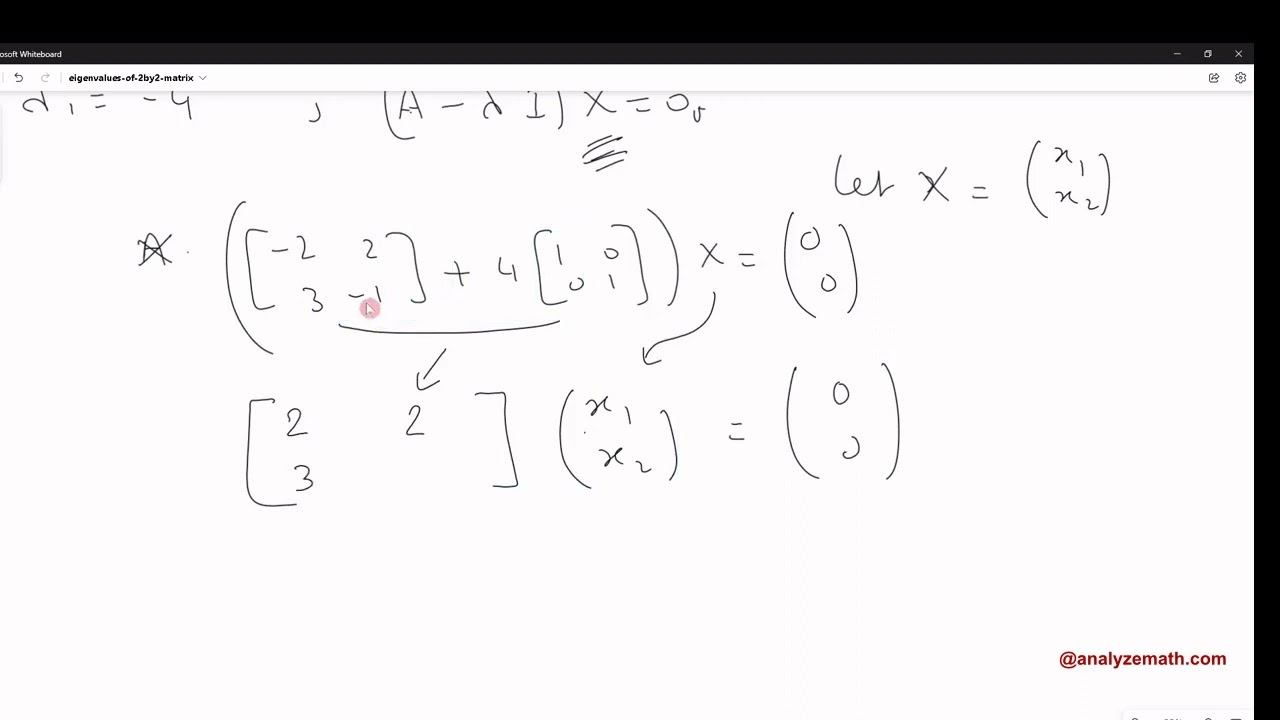
Eigenvalues and Eigenvectors of a 2 by 2 Matrix
The video starts with the necessary definitions of parallel vectors and the eigenvalues and eigenvectors using numerical examples. Then the calculations start with the main equation of eigenvectors: AX = Lambda X. The condition of the determinant of the

Eigenvalues and Eigenvectors of a 3 by 3 Matrix
This video is about calculating the eigenvalues and eigenvectors of a 3 by 3 matrix. It includes 5 learning objectives: 1 - Review of Eigenvalues and Eigenvectors - 2 - Review the equation A V = Lambda V, which defines the Eigenvalues and Eigenvectors
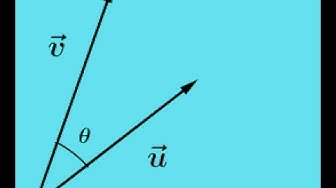
Use Dot Product to Find the Angle between Two vectors
The dot product is used to find the angle between two 3D vectors. more at: www.analyzemath.com/high_school_math/grade_12/scal_cross.html

Calculate the Determinant of a 3 by 3 Matrix
This video presents the steps needed to find the determinant of a 3 by 3 matrix using determinants of 2 by 2 matrices.